Model nelineárneho mechatronického systému
Fyzikálny model nelineárneho mechatronického systému
Inverzné kyvadlo je jedným z často využívaných modelov na testovanie a overovanie rôznych typov algoritmov riadenia. Nakoľko ide o nelineárny model, spravidla sa riadenie skladá z dvoch prepínateľných algoritmov: algoritmus na vyhodenie kyvadla do hornej rovnovážnej polohy a algoritmus na „zachytenie“ kyvadla a jeho udržanie v hornej rovnovážnej polohe.
Fyzikálny model nelineárneho mechatronického systému:

Virtuálny model nelineárneho mechatronického systému:
Matematický model sústavy
Pre odvodenie matematického modelu inverzného kyvadla je vhodné rozdeliť si sústavu na dva podsystémy, ako je znázornené na obr.
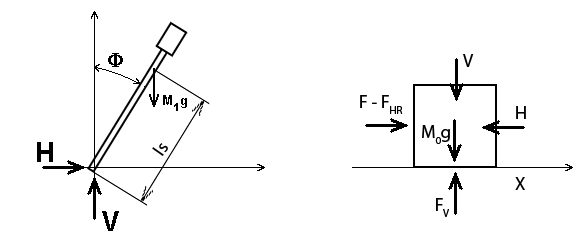
Podsystémy sústav kyvadla (naľavo) a vozíka (napravo)
Hmotnosť kyvadla je označená ako M1 a lS je vzdialenosť ťažiska kyvadla od jeho osi otáčania. Ak r označuje polohu vozíka, potom horizontálnu silu pôsobiacu na spodný bod kyvadla môžeme vyjadriť nasledovne
![]()
Táto sila je spôsobená zrýchlením ťažiska. Jej vertikálna zložka je
![]()
Zo zákona zachovania hybnosti môžeme vyjadriť rotačný pohyb tyče okolo jej ťažiska
![]()
pričom ΘS vyjadruje moment zotrvačnosti kyvadla vzhľadom na ťažisko. C je konštanta viskózneho trenia kyvadla. Pohybovú rovnicu pre systém vozíka môžeme napísať takto
![]()
Hmotnosť vozíka je označená ako M0 a Fr je konštanta viskózneho trenia vozíka. Sila pôsobiaca prostredníctvom prevodového pásu je F. Derivovaním rovníc dostávame
![]()
a
![]()
Po dosadení predchádzajúcich rovníc eliminujeme premenné V a H. Po priamych úpravách môžeme napísať dve nelineárne diferenciálne rovnice
![]()
a
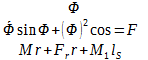
Pre zjednodušenie sme použili substitúcie
![]()
Tieto rovnice tvoria základ pre modelovanie inverzného kyvadla.
Vstupy/výstupy
Vstup: želaná pozícia
Výstup: aktuálna pozícia kyvadla
Úloha:
Cieľom je návrh algoritmu robustného riadenia na udržanie kyvadla v hornej polohe.